Preprints
2025
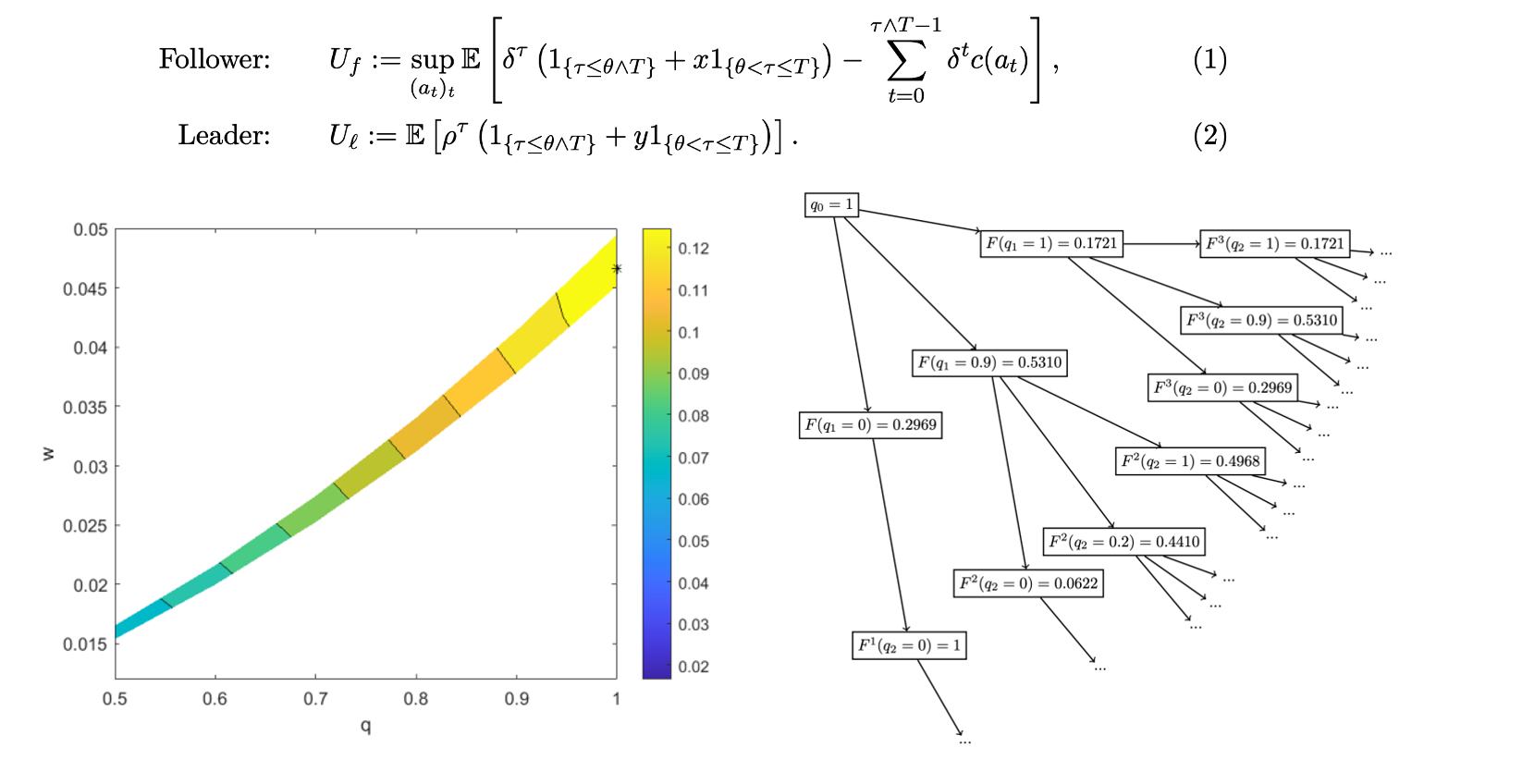
Optimal Information Disclosure In A Stackelberg GameRuyi Liu and Zhou ZhouSSRN preprint, 2025We investigate a leader-follower game in which the leader hires the follower to complete a project with the presence of a random shock time. If the project is completed before the shock time, then both players receive (up to discounting) 1 each. If it is completed after the shock time, then the leader and the follower receive y and $x respectively. The shock time is observable by the leader, but not by the follower. The leader chooses how to reveal the information of the shock time, and the follower controls the effort level which affects the project completion time. The goal is to find the leader’s value and optimal information disclosure strategy. By considering the leader’s value as a function of the follower’s utility as well as the follower’s belief about the shock time, we characterize the leader’s value using dynamic programming equations. The leader’s (ε-)optimal strategy can also be constructed from these equations.
2024
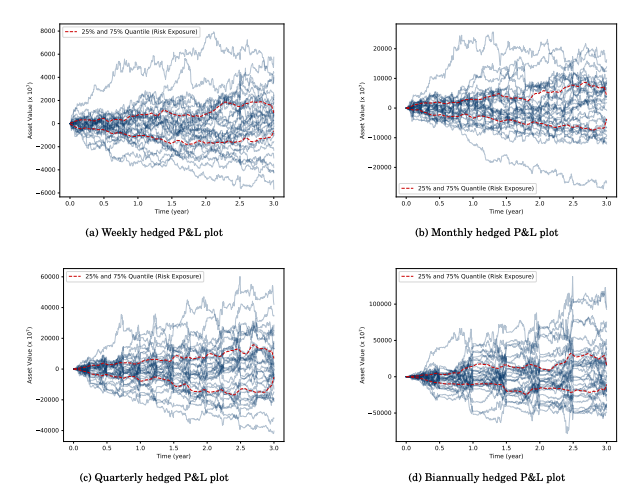
Cross-Currency Basis Swaps Referencing Backward-Looking RatesYining Ding, Ruyi Liu, and Marek Rutkowskiarxiv preprint, 2024The financial industry has undergone a significant transition from the London Interbank Offered Rate (LIBOR) to Risk Free Rates (RFR) such as, e.g., the Secured Overnight Financing Rate (SOFR) in the U.S. and the AUD Overnight Index Average (AONIA) in Australia, as the primary benchmark rate for borrowing costs. The paper examines the pricing and hedging method for SOFR-related financial products in a cross-currency context with the special emphasis on the Compound SOFR vs Average AONIA cross-currency basis swaps. While the SOFR and AONIA serve as a particular case of a cross-currency basis swap (CCBS), the approach developed is able to handle backward-looking term rates for any two currencies. We give explicit pricing and hedging results for collateralized cross-currency basis swaps using interest rate and currency futures contracts as hedging tools within an arbitrage-free multi-curve setting.
Journal Papers
2025
Vulnerable European and American options in a market model with optional hazard processLibo Li, Ruyi Liu, and Marek RutkowskiAccepted by Finance and Stochastics, 2025We study the upper and lower bounds for prices of European and American style options with the possibility of an external termination, meaning that the contract may be terminated at some random time. Under the assumption that the underlying market model is incomplete and frictionless, we obtain duality results linking the upper price of a vulnerable European option with the price of an American option whose exercise times are constrained to times at which the external termination can happen with a non-zero probability. Similarly, the upper and lower prices for an vulnerable American option are linked to the price of an American option and a game option, respectively. In particular, the minimizer of the game option is only allowed to stop at times which the external termination may occur with a non-zero probability.
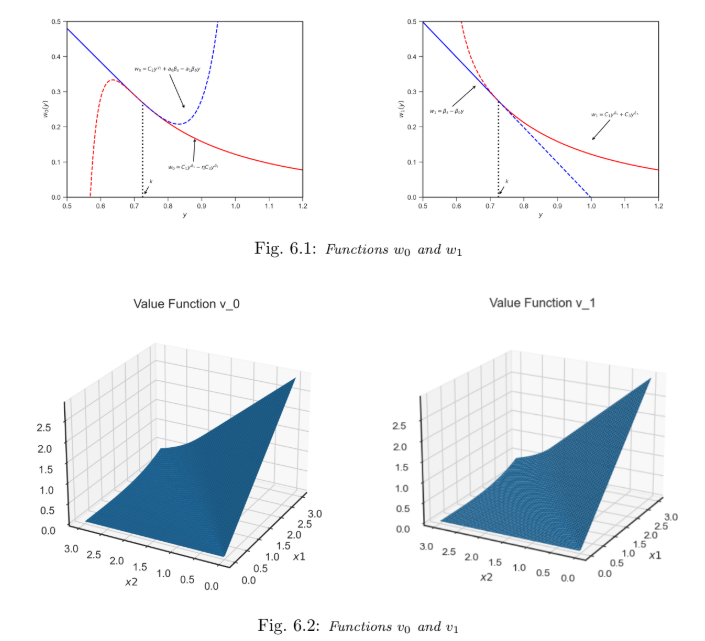
Pairs trading: An optimal selling rule with constraintsRuyi Liu, Jingzhi Tie, Zhen Wu, and Qing ZhangCommunications in Mathematical Sciences, 2025The main focus of this paper is to identify the most effective selling strategy for pairs trading of stocks. In pairs trading, a long position is held in one stock meanwhile a short position is held in another. The goal is to determine the optimal time to sell the long position and repurchase the short position in order to close the pair position. The paper presents an optimal pairs-trading selling rule with trading constraints. In particular, the underlying stock prices evolve according to a two-dimensional geometric Brownian motion and the trading permission process is given in terms of a two-state trading allowed, trading not allowed Markov chain. It is shown that the optimal policy can be determined by a threshold curve which is obtained by solving the associated Hamilton-Jacobi-Bellman (HJB) equations (quasi-variational inequalities). A closed-form solution is obtained. A verification theorem is provided. Numerical experiments are also reported to demonstrate the optimal policies and value functions.
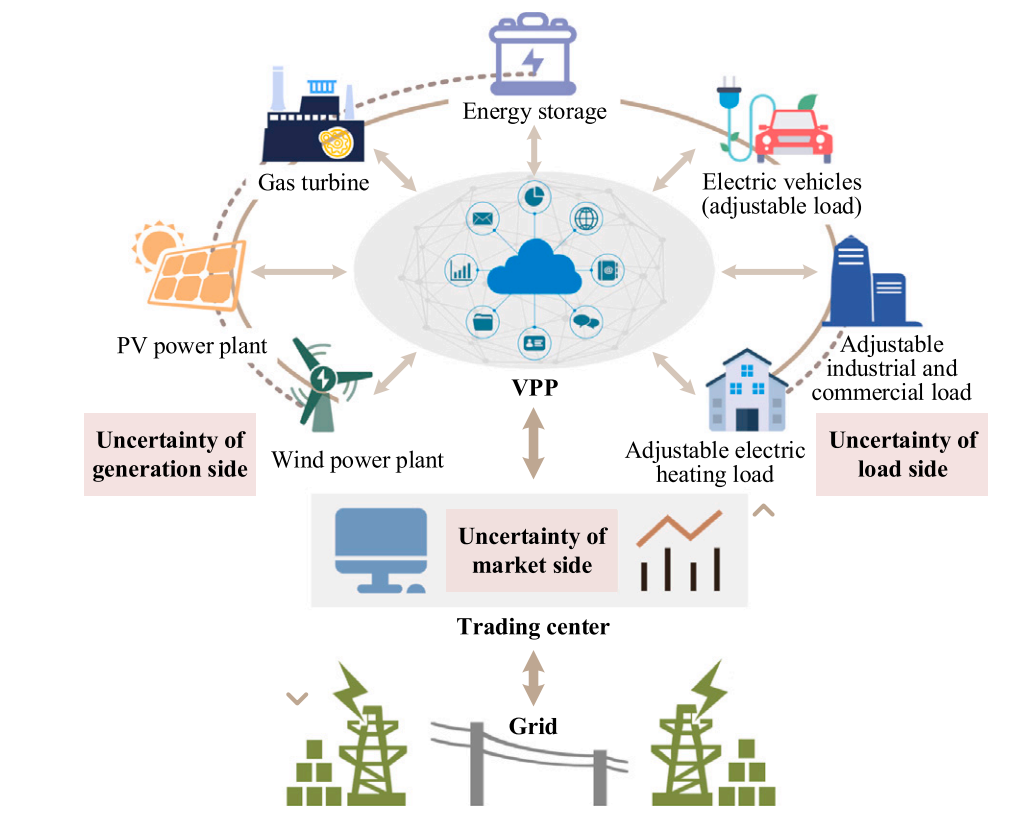
Data-Driven interval robust optimization method of VPP Bidding strategy in spot market under multiple uncertaintiesYing Ma, Zhen Li, Ruyi Liu, Bin Liu, and al.Applied Energy, 2025The participation of Virtual Power Plants (VPPs) in the spot market enhances the flexibility of modern power systems as renewable energy penetration increases. However, multiple uncertainties on the market, load, and generation sides can significantly affect the bidding strategies and operational efficiency of VPPs. This paper employs interval numbers generated by a data-driven model to capture the uncertainty and correlation of electricity prices in the spot market. Additionally, uncertainty sets are utilized to represent the variability in the number of electric vehicles (EVs) and photovoltaic (PV) power generation. A two-stage interval robust optimization model considering arbitrage opportunity is established to optimize the bidding strategies of a VPP that includes gas turbines, energy storage, PV systems, and EVs. An improved column-and-constraint generation (C&CG) algorithm is developed to solve this model. The results demonstrate that the interval numbers of electricity prices produced by the proposed data-driven model can reduce VPP cost fluctuations by 9.3%. The two-stage interval robust optimization model reduces costs by 2.5% compared to a single-stage robust method and 52.0% compared to robust method ignoring arbitrage opportunities. As parameters change, the advantages of the proposed model become more significant. The improved C&CG algorithm shows superior convergence and accuracy. Unlike stochastic optimization methods that generate scenarios, the computational time for the interval optimization method can be reduced to. This study offers a feasible solution for the bidding strategies of VPPs considering multiple uncertainties in the spot market.
2024
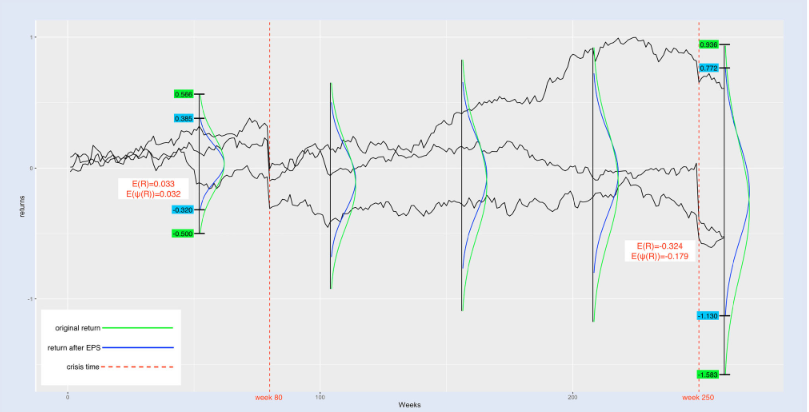Equity protection swaps: investment insurance for superannuation accounts.Huansang Xu, Ruyi Liu, and Marek RutkowskiQuantitative Finance, 2024A novel type of an investment insurance product for holders of superannuation accounts in Australia, tentatively named an Equity Protection Swap (EPS), is proposed and examined. An EPS shares some features with the variable annuity known as the registered index-linked annuity (RILA) but it is a standalone financial derivative, which makes it appropriate as a protection tool against downside risk for holders of superannuation accounts. Its basic forms, dubbed buffer and floor EPSs, offer a partial protection against losses on a reference portfolio below a predetermined threshold in exchange for a share of portfolio’s gains if the realised return on a reference portfolio is above a predetermined level. Model-free explicit pricing formula for a generic EPS is obtained by considering its static hedging by a portfolio of European options. As opposed to classical insurance products, the structure of an EPS allows for the fair initial premium to be null through a judicious selection of the provider’s participation rate in portfolio’s gains. A theoretical study of forward performance of EPSs based on the cross-currency market model and an empirical cost/benefit analysis based on market data for S&P 500 and S&P/ASX 200 indices demonstrate tangible benefits of EPSs as an efficient investment insurance tool for superannuation accounts.
Penalization schemes for BSDEs and reflected BSDEs with generalized driverLibo Li, Ruyi Liu, and Marek RutkowskiProbability, Uncertainty & Quantitative Risk, 2024The paper is directly motivated by the pricing of vulnerable European and American options in a general hazard process setup and a related study of the corresponding pre-default backward stochastic differential equations (BSDE) and pre-default reflected backward stochastic differential equations (RBSDE). The goal of this work is twofold. First, we aim to establish the well-posedness results and comparison theorems for a generalized BSDE and a reflected generalized BSDE with a continuous and nondecreasing driver . Second, we study penalization schemes for a generalized BSDE and a reflected generalized BSDE in which we penalize against the driver in order to obtain in the limit either a constrained optimal stopping problem or a constrained Dynkin game in which the set of minimizer’s admissible exercise times is constrained to the right support of the measure generated by A .
2023
Continuous-time mean-variance portfolio selection under non-Markovian regime-switching model with random horizontian Chen, Ruyi Liu, and Zhen WuJournal of Systems Science and Complexity, 2023This paper considers a continuous-time mean-variance portfolio selection with regime-switching and random horizon. Unlike previous works, the dynamic of assets are described by non-Markovian regime-switching models in the sense that all the market parameters are predictable with respect to the filtration generated jointly by Markov chain and Brownian motion. The Markov chain is assumed to be independent of Brownian motion, thus the market is incomplete. The authors formulate this problem as a constrained stochastic linear-quadratic optimal control problem. The authors derive closed-form expressions for both the optimal portfolios and the efficient frontier. All the results are different from those in the problem with fixed time horizon.
Two Equivalent Families of Linear Fully Coupled Forward Backward Stochastic Differential EquationsRuyi Liu, Zhen Wu, and Detao ZhangESAIM: Control, Optimisation and Calculus of Variations, 2023In this paper, we investigate two families of fully coupled linear Forward-Backward Stochastic Differential Equations (FBSDEs) and its applications to optimal Linear Quadratic (LQ) problems. Within these families, one could get same well-posedness of FBSDEs with totally different coefficients. A family of FBSDEs is proved to be equivalent with respect to the Unified Approach. Thus one could get well-posedness of whole family once a member exists a unique solution. Another equivalent family of FBSDEs are investigated by introducing a linear transformation method. Owing to the coupling structure between forward and backward equations, it leads to a highly interdependence in solutions. We are able to decouple FBSDEs into partial coupling, by virtue of linear transformation, without losing the existence and uniqueness to solutions. Moreover, owing to non-degeneracy of transformation matrix, the solution to original FBSDEs is totally determined by solutions of FBSDEs after transformation. In addition, an example of optimal LQ problem is presented to illustrate.
2021
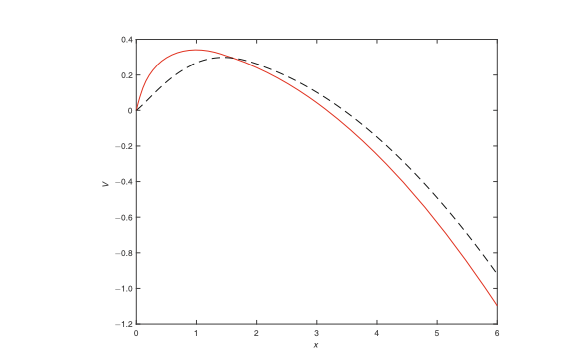An optimal pricing policy under a Markov chain modelRuyi Liu, Jingzhi Tie, Zhen Wu, and Qing ZhangScience China Mathematics, 2021This paper is about an optimal pricing control under a Markov chain model. The objective is to dynamically adjust the product price over time to maximize a discounted reward function. It is shown that the optimal control policy is of threshold type. Closed-form solutions are obtained. A numerical example is also provided to illustrate our results.
2020
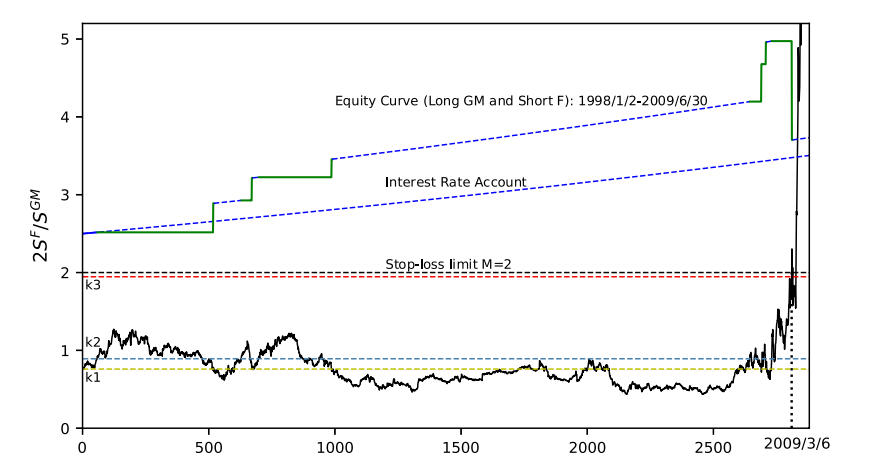Pairs-Trading under Geometric Brownian Motions: An Optimal Strategy with Cutting LossesRuyi Liu, Zhen Wu, and Qing ZhangAutomatica, 2020Pairs trading is about simultaneously trading a pair of stocks. A pairs trade is triggered when their prices diverge and consists of a short position of the strong stock and a long position of the weak one. Pairs trading bets on the reversal of their price strengths. In this paper, we study the optimal pairs-trading problem under general geometric Brownian motions and focus on trading with cutting losses. The objective is to trade the pairs over time to maximize an overall return with a fixed transaction cost. Our optimal policy is characterized by threshold curves obtained by solving the associated HJB equations. We provide sufficient conditions that guarantee the optimality of our trading rules. We also present numerical examples to illustrate.
2019
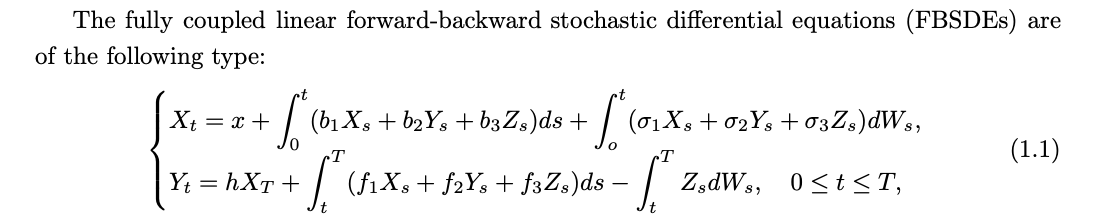Well-posedness of fully coupled linear forward-backward stochastic differential equationsRuyi Liu and Zhen WuJournal of Systems Science and Complexity, 2019This paper studies the well-posedness of fully coupled linear forward-backward stochastic differential equations (FBSDEs). The authors introduce two main methods-the method of continuation under monotonicity conditions and the unified approach-to ensure the existence and uniqueness of solutions of fully coupled linear FBSDEs. The authors show that the first method (the method of continuation under monotonicity conditions) can be deduced as a special case of the second method (the unified approach). An example is given to illustrate it in linear FBSDEs case. And then, a linear transformation method in virtue of the non-degeneracy of transformation matrix is introduced for cases that the linear FBSDEs can not be dealt with by the the method of continuation under monotonicity conditions and the unified approach directly. As a powerful supplement to the the method of continuation under monotonicity conditions and the unified approach, linear transformation method overall develops the well-posedness theory of fully coupled linear forward-backward stochastic differential equations which have potential applications in optimal control and partial differential equation theory.
Well-posedness of a class of two-point boundary value problems associated with ordinary differential equationsRuyi Liu and Zhen WuAdvances in Difference Equations, 2019This paper introduces the regular decoupling field to study the existence and uniqueness of solutions of two-point boundary value problems for a class of ordinary differential equations which can be derived from the maximum principle in optimal control theory. The monotonicity conditions used to guarantee the existence and uniqueness of such equations are initially a special case of the regular decoupling field method. More generally, in case of the homogeneous equations, this paper generalizes the application scope of the monotonicity conditions method by using the linear transformation method. In addition, the linear transformation method can be used to handle the situation where the monotonicity conditions and regular decoupling field method cannot be directly applied. These two methods overall develop the well-posedness theory of two-point boundary value problems which has potential applications in optimal control and partial differential equation theory.